Para este segundo parcial de ven las características de los líquidos, sus propiedades y leyes que los rigen, principalmente el concepto de presión, ya que con este se inicia con la aplicación de los Principios de Pascal y de Arquímedes y la flotación de los cuerpos. Se analizarán las aplicaciones de la Hidrodinámica y los conceptos de gasto, flujo y la ecuación de continuidad para con ello poder aplicar los principios de Bernoulli y Torricelli.

1. principio de arquímedes

El principio de Arquímedes nos indica que “todo cuerpo sumergido dentro de un fluido experimenta una fuerza ascendente llamada empuje, equivalente al peso del fluido desalojado por el cuerpo”.

Este principio lo aplicamos cuando nadamos, cuando tiramos un objeto al agua; el objeto se hunde si su peso es mayor que el peso del fluido desalojado (desplazado). El objeto flota cuando su peso es menor o igual al peso del fluido desplazado.

El empuje que recibe cualquier cuerpo sumergido será igual al volumen sumergido multiplicado por el peso específico del fluido que se trate, es decir:

El peso del cuerpo (P) sea igual a la fuerza del empuje (E), entonces el cuerpo se mantiene en equilibrio dentro del líquido.
El peso del cuerpo (P) es mayor que la fuerza de empuje (E), entonces el cuerpo se hunde hasta encontrar algo que lo sostenga.
El peso del cuerpo (P) es menor que la fuerza de empuje (E), entonces el cuerpo flota, es decir, algo de él queda en la superficie del líquido.

Hagamos un ejercicio

2. Ecuación de continuidad

Es importante poder determinar la cantidad de un líquido que fluye a través de tuberías y, también, el cambio de presión en las mismas al aumentar o disminuir su sección transversal, entre otras propiedades.

Con objeto de facilitar el estudio de los líquidos en movimiento, generalmente se hacen las siguientes suposiciones:

Los líquidos son prácticamente incompresibles.
Se supone a los líquidos como ideales. Es decir, se considera despreciable la viscosidad. Por ello se supone que no presentan resistencia al flujo, lo cual permite despreciar las pérdidas de energía mecánica producidas por su viscosidad; dado que, durante el movimiento ésta genera fuerzas tangenciales entre las diferentes capas de un líquido.
El flujo de los líquidos se supone estacionario o de régimen estable. Esto sucede cuando la velocidad de toda partícula del líquido es igual al pasar por el mismo punto.

Gasto

Es el volumen de fluido que pasa a través del área de la sección transversal de un tubo, en la unidad de tiempo. Lo anterior quiere decir que el gasto es la relación que existe entre el volumen de líquido que fluye por un conducto y el tiempo que tarda en fluir.

La representación matemática de la definición anterior es:

Ecuación de la continuidad

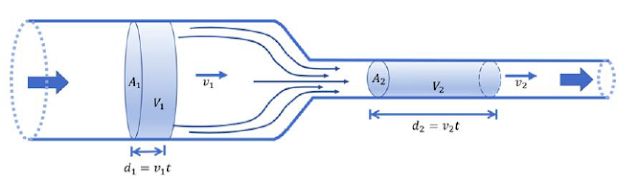
Al reducir el diámetro de la sección transversal de un tubo, se obtiene un aumento en la velocidad del fluido.

Analicemos, detenidamente, la figura siguiente.

Checa los ejercicios realizados en clase

3. teorema de bernoulli

Suponiendo el movimiento de un líquido de régimen estable, incompresible y no viscoso, a través de un tubo, se puede despreciar la pérdida de energía como resultado de la fricción interna entre sus partículas. Si el tubo es de sección transversal variable, el líquido sufrirá una aceleración y una desaceleración, por lo que, su velocidad cambiará. Esto implica que está sometido a una fuerza resultante, lo que significa una variación de presión a lo largo del tubo.

Este problema lo estudió por primera vez Daniel Bernoulli en 1738, en su tratado de Hidrodinámica, creando lo que conocemos como Principio de Bernoulli

La conservación de la energía, o el teorema general del trabajo-energía, nos lleva a una relación muy general para el flujo de fluidos. El primero en deducir esta relación fue el matemático suizo Daniel Bernoulli (1700-1782).

“El trabajo total externo, aplicado a un sistema de flujo estacionario de un fluido ideal, es igual al cambio de la energía mecánica del sistema”.

El Principio de Bernoulli establece que:

La suma de las energías cinética y potencial y de presión que tiene el líquido en un punto, es igual a la suma de estas energías en otro punto cualquiera, y la ecuación que representa a dicho Principio es: